Ecuaciones de primer grado resueltas y explicadas
Resolvemos detalladamente 10 ecuaciones de primer grado. Recordad que, si existe, la solución de una ecuación es el número (o números) que tiene que tomar la incógnita \(x\) para que la identidad sea verdadera.
Por ejemplo, la solución de la ecuación \(2·x = x+1\) es \(x=1\) porque al cambiar \(x\) por \(1\), tenemos una igualdad verdadera:

En cambio, \(x=3\) no sería solución ya que

Recordad:
- Tenemos que sumar/restar los números con los números y las \(x\) con las \(x\).
- Lo que suma en un lado, pasa al otro lado restando, y viceversa.
- Lo que multiplica en un lado, pasa al otro lado dividiendo, y viceversa.
- No podemos multiplicar ni dividir entre \(x\).
- Los paréntesis sirven para agrupar una misma operación.
- Para evitar las fracciones, podemos multiplicar toda la ecuación por el mínimo común múltiplo de los denominadores.
Más ejemplos en ecuaciones resueltas.
Ecuación 1

Solución:
El \(2\) que suma en el lado izquierdo, pasa al lado derecho restando:
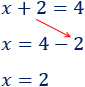
La solución de la ecuación es \(x = 2\).
Ecuación 2
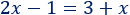
Solución:
El \(1\) de la izquierda pasa sumando a la derecha:
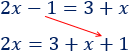
La \(x\) de la derecha pasa restando a la izquierda:
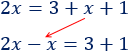
Sumamos las \(x\) (izquierda) y los números (derecha):
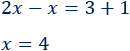
La solución es \(x = 4\).
Ecuación 3
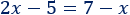
Solución:
El \(5\) pasa sumando a la derecha:
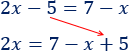
La \(x\) de la derecha pasa sumando a la izquierda:
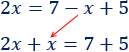
Sumamos las \(x\) y los números:
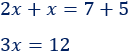
El número \(3\) que hay delante de la \(x\) está multiplicando, así que pasa al otro lado dividiendo:
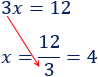
La solución es \(x=4\).
Ecuación 4
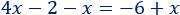
Solución:
El \(2\) pasa sumando al otro lado:
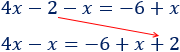
La \(x\) de la derecha pasa al otro lado restando:
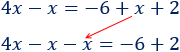
Sumamos las \(x\) y los números:
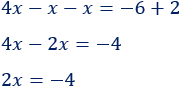
El \(2\) pasa dividiendo al otro lado:
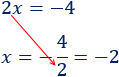
La solución es \(x = -2\).
Ecuación 5
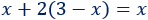
Solución:
El \(2\) que hay delante del paréntesis multiplica a todo lo que éste contiene:
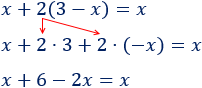
Pasamos el \(6\) restando al otro lado:
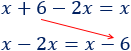
Pasamos la \(x\) de la derecha al otro lado:
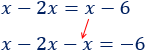
Operamos:
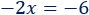
El \(-2\) pasa dividiendo al otro lado:
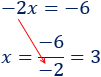
La solución es \(x = 3\).
Ecuación 6

Solución:
El signo negativo que hay delante del paréntesis cambia los signos que ésye tiene dentro:
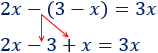
Pasamos \(3x\) y \(3\) al otro lado:
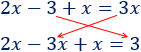
Sumamos:
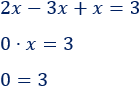
La ecuación no tiene solución porque hemos obtenido una igualdad falsa.
Ecuación 7
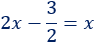
Solución:
Como tenemos una fracción, podemos multiplicar toda la ecuación por el denominador para eliminarla:
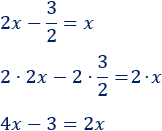
Cambiamos de lado \(2x\) y \(3\):
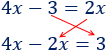
Resolvemos:
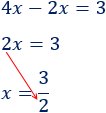
La solución es \(x = 3/2\).
Ecuación 8
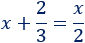
Solución:
Tenemos dos denominadores distintos, así que multiplicamos la ecuación por el mínimo común múltiplo de los denominadores (es 6) para eliminar las fracciones:
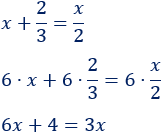
Resolvemos:
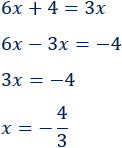
La solución es \(x=-4/3\).
Ecuación 9
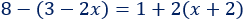
Solución:
En la izquierda, el signo negativo del paréntesis cambia los signos de su contenido:
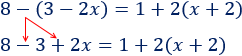
En la derecha, el \(2\) que hay delante del paréntesis multiplica su contenido:
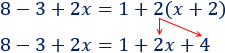
Resolvemos la ecuación:
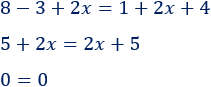
Cuando llegamos a una igualdad que es verdadera, la solución es todos los reales. Es decir, cualquier número real es solución de la ecuación:

Ecuación 10
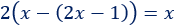
Solución:
Tenemos un paréntesis dentro del otro. Eliminamos primero el de dentro, cambiando el signo de su contenido:
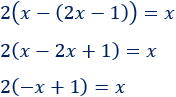
Multiplicamos el paréntesis por \(2\):
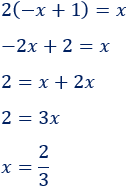
La solución de la ecuación es \(x = 2/3\).