Máximo común divisor y mínimo común múltiplo
Problemas de mcd y mcm
Explicamos los conceptos de mcd y mcm, cómo calcularlos y resolvemos algunos problemas de aplicación para mostrar su utilidad práctica.
Enlaces relacionados:
1. Concepto de mcm y mcd
El máximo común divisor (mcd) de dos números \(a\) y \(b\) es el número natural más grande que es divisor de \(a\) y de \(b\).
Por ejemplo, vamos a calcular el mcd de 30 y 42. Los divisores de 30 y 42 son los siguientes:

Los divisores comunes son 1, 2, 3 y 6. El mayor de éstos es 6.
Por tanto, el mcd de 30 y 42 es 3.
El mínimo común múltiplo (mcm) de dos números \(a\) y \(b\) es el número natural más pequeño que es múltiplo de \(a\) y de \(b\).
Por ejemplo, vamos a calcular el mcm de 6 y 15. Los primeros múltiplos de 6 y 15 son los siguientes:
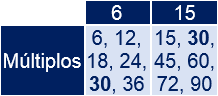
El múltiplo común más pequeño es 30, así que el mcm de 6 y 15 es 30.
2. Cálculo de mcm y mcd
La forma más rápida de calcular el mcm y el mcd es escribir los números como productos de potencias de números primos. Entonces,
-
El mcd es el producto de las potencias cuyas bases son comunes, con el exponente menor.
-
El mcm es el producto de las potencias con bases comunes y no comunes, con el exponente mayor.
Por ejemplo, las descomposiciones de 60 y 72 son
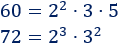
El mcd es
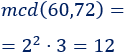
El mcm es
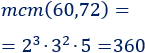
Problema 1
Tenemos una cuerda que mide 24cm y otra que mide 32cm y queremos cortarlas en trozos iguales y que sean los más grande posible. ¿Cuánto debe medir cada trozo?
Solución:
La longitud de los trozos tiene que ser un divisor de 24 y de 32 para que todos los trozos midan lo mismo. Además, debe ser máximo.
Tenemos que calcular el mcd de 24 y 32:
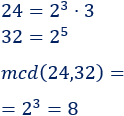
Cada trozo debe medir 8cm.
De una cuerda se obtienen 3 trozos y de la otra, 4. En total, 7 trozos de 8cm.
Problema 2
Amílcar da una vuelta a la manzana en 3 minutos y Mateo lo hace en 4. Si parten del mismo punto y en el mismo momento, ¿cuánto tiempo tardarán en encontrarse en el punto de salida?
Solución:
Amílcar pasa por la salida cada 3 minutos, es decir, en el minuto 3, 6, 9, 12, 15, 18…
Mateo lo hace cada 4 minutos, es decir, en el minuto 4, 8, 12, 16, 20, 24…
Los tiempos calculados son los múltiplos de 3 y 4. Mateo y Amílcar coinciden, por primera vez, en el minuto 12.
Hemos calculado el mcm de 3 y 4.
Problema 3
Arturo tiene una caja con 48 pelotas de tenis y una caja con 84 pelotas de beisbol para repartirlas entre sus amigos. Desea que cada amigo tenga la misma cantidad de pelotas de tenis y de beisbol y dárserlas al máximo número posible de amigos. ¿Cuántas pelotas debe dar a cada amigo?
Solución:
El número de amigos tiene que ser el mayor posible y divisor del número de pelotas.
Tenemos que calcular el mcd:
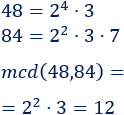
Puede dar a 12 de sus amigos.
Arturo debe dar 4 pelotas de tenis y 7 de beisbol a cada uno de los 12 amigos.
Problema 4
Josué quiere tener un bate por cada pelota de beisbol. Si los bates se venden en cajas de 6 unidades y las pelotas, en cajas de 20, ¿cuál es el número mínimo de cajas que debe comprar para tener tantos bates como pelotas?
Solución:
Tenemos que calcular el mcm:
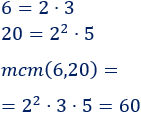
Josué debe comprar 60 bates y 60 pelotas, es decir, 10 cajas de bates y 3 cajas de pelotas.