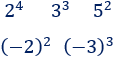%| Calcular porcentaje online

7 calculadoras de porcentajes

Instrucciones: Escribir los datos en los cuadros y pulsar el botón Calcular para ver el resultado en el cuadro amarillo. En caso de decimales, se aproxima con 2 cifras (por ejemplo, si el resultado es 10.998, la calculadora proporciona 11). Las calculadoras escriben los datos en una tabla y aplican una regla de tres simple, mostrando las operaciones y una barra de porcentajes.

Recordatorio (teoría)

  • El porcentaje es una forma de referirse a una proporción tomando como referencial el número 100.

  • Para calcular un porcentaje, identificamos el total de individuos con el 100%.

  • El porcentaje \(n\%\) significa \(n\) individuos de cada 100.

Ejemplos:

  • El 50% es la mitad del total (50 de cada 100).

  • El 25% es la cuarta parte del total (25 de cada 100).

  • El 20% es la quinta parte del total (20 de cada 100).

Para calcular porcentajes, aplicamos una regla de tres simple, puesto que se trata de una relación de proporcionalidad directa.

Problemas resueltos de porcentajes:

Calculadora 1

Descripción: calcular el porcentaje de una cantidad dada.

El % de es .


Operaciones

\(n\) %
\( x \)
20
200
 100

$$x = \frac{20·200}{100} = 40$$

Representación

↓40
0
200
20%

Ejemplos: Problemas fáciles resueltos de porcentajes

Calculadora 2

Descripción: calcular el total conociendo un porcentaje.

Si el % es , entonces el total es .

Operaciones

\(n\) %
20
10
\(x\) 100

$$x = \frac{20·100}{10} = 200$$

Representación

↓20
0
200
10%

Calculadora 3

Descripción: calcular qué porcentaje del total es una cantidad.

Si el total es, entonces es el %.

Operaciones

\(n\) %
40
 \(x\)
200
 100

$$ x = \frac{40·100}{200} = 20\% $$

Representación

↓40
0
200
20%

Calculadora 4

Descripción: calcular un porcentaje a partir de otro porcentaje.

Si el % es , entonces el % es .

Operaciones

\(n\) %
10
60
\(x\)
30

$$ x = \frac{10·30}{60} = 5 $$

Representación

↓5
0
16.67
30%

Calculadora 5

Descripción: calcular el precio final tras aplicar un porcentaje de descuento.

Si el precio inicial es € y se aplica un descuento del %, el precio final es €.    

Operaciones

€ %
60
 100
\(x\)
90

$$ x = \frac{60·90}{100} = 54€$$
Descuento: 6€

Representación

↓54
0
60
90%

Ejemplos: Problemas resueltos de descuentos

Calculadora 6

Descripción: calcular el precio final tras aplicar un porcentaje de aumento.

Si el precio inicial es € y se aplica un aumento del %, el precio final es €.   

Operaciones

€ %
60
 100
\(x\)
110

$$ x = \frac{60·110}{100} = 66€$$
Aumento: 6€

Ejemplos: Problemas resueltos de aumentos

Calculadora 7

Descripción: calcular el porcentaje aplicado al precio inicial conociendo el precio final. Si el porcentaje es negativo, se trata de un descuento.

Si el precio inicial era € y el precio final es €, se ha aplicado un %.

Operaciones

€ %
10
 100
5
 \(x\)

$$ x = \frac{5·100}{10} = 50\%$$
Aplicado: -50%
Diferencia: -5€

Problemas resueltos

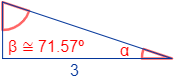
A continuación, se proporciona una colección de problemas resueltos sobre porcentajes y una colección de problemas resueltos de otros temas matemáticos (como el teorema de Pitágoras o las propieddes de las potencias).

Problemas de calcular porcentajes

Ejemplo de problema:

Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?

Problemas de porcentajes de aumentos

Ejemplo de problema:

El año pasado se vendieron 1200 videojuegos y 980 libros. Si este año subió un 15% la venta de videojuegos y subió un 5% la de libros, ¿cuántos videojuegos y libros se vendieron?

Problemas de porcentajes de descuentos

Ejemplo de problema:

La población de una ciudad pasó de 10 millones de habitantes a 9 millones en tan solo un año. ¿Qué porcentaje de decrecimiento poblacional hubo?

Problemas de porcentajes de aumentos y descuentos

Ejemplo de problema:

El sueldo de Andrés en 2010 era de 1200€ mensuales y en 2015 era de 1620€. ¿Qué porcentaje aumentó en esos 5 años?

Problemas de porcentajes mayores que 100%

Ejemplo de problema:

Alberto vendió una antigüedad recuperando el precio que pagó por ella más un 36% de beneficio. Si la vendió por 476€, ¿cuánto pagó por ella?

Problemas de porcentajes de diferencia o error

Ejemplo de problema:

¿Cuál es el porcentaje de diferencia (con signo) de los beneficios de una empresa si han antes eran 120 millones anuales y ahora son 108 millones?

Problemas de calcular porcentajes multiplicando por un decimal


Ejemplo de problema:

Calcular el 50% del 30% de 360. ¿Qué porcentaje de 360 es?

Problemas de porcentajes de porcentajes


Ejemplo de problema:

¿Qué porcentaje es el 60% del 70%? ¿Es el mismo porcentaje que el 70% del 60%?

Problemas variados de porcentajes


Ejemplo de problema:

Tras un aumento del 25%, el sueldo actual de Leo es de 1625€ mensuales. ¿Cuál era su sueldo anterior?

Conversión entre porcentajes y fracciones


Ejemplo de problema:

Escribir los siguientes porcentajes como fracciones: 25%, 35%, 72%, 24.2%, 71.52% y 5.55%.

Problemas de Pitágoras

Ejemplo de problema:

¿Cuánto mide la hipotenusa de un triángulo rectángulo si sus dos catetos miden 1cm?

Ecuaciones de primer grado

Ejemplo de problema:

Resolver la siguiente ecuación:

Ecuaciones de primer grado

Problemas de ecuaciones

Ejemplo de problema:

Hace 3 años, la edad de Raúl era el doble de la edad que tenía hace 5 años. ¿Qué edad tiene Raúl?

Sistemas de ecuaciones

Ejemplo:

Resolución del siguiente sistema por el método de sustitución:

sistemas de ecuaciones

Problemas de sistemas de ecuaciones

Ejemplo de problema:

Un rectángulo tiene perímetro 8 metros y su altura es el triple que su base. ¿Cuál es la altura del rectángulo?

Problemas de trigonometría

Ejemplo de problema:

Calcular la hipotenusa del siguiente rectángulo:

problemas de trigonometría

Propiedades de las potencias

Ejemplo de problema:

Calcular las siguientes potencias:

Propiedades de las potencias

Mcd y mcm

Ejemplo de problema:

Tenemos una cuerda que mide 24cm y otra que mide 32cm y queremos cortarlas en trozos iguales y que sean los más grande posible. ¿Cuánto debe medir cada trozo?


Calcular porcentaje online ©

ISBN: 978-84-09-14645-1