Problemas resueltos de sistemas de ecuaciones
Resolvemos problemas mediante un sistema de ecuaciones lineales de 2 ecuaciones con 2 incógnitas.
Como lo importante es plantear el sistema de ecuaciones, no resolvemos detalladamente los sistemas. Más información sobre los métodos en sistemas de ecuaciones.
Método de resolución:
- Obtener los datos
- Identificar las incógnitas \(x\) e \(y\)
- Plantear el sistema de dos ecuaciones
- Resolver el sistema
Más ejemplos en problemas de sistemas de ecuaciones.
Problema 1
Hallar dos números sabiendo que su suma es 15 y su resta es 3.
Solución:
Incógnitas:
- \(x\) es uno de los números
- \(y\) es el otro número
Ecuaciones:
La suma de los números es 15:
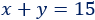
La resta de los números es 3:
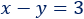
Sistema de ecuaciones:
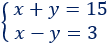
La solución del sistema es
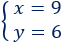
Por tanto, los números son 9 y 6.
Problema 2
Miguel es mayor que su hermana María. Dentro de 3 años, la edad de María será la edad que tiene ahora Miguel y, dentro de 10 años, la edad de Miguel será el doble de la edad que tiene María. ¿Qué edades tienen los hermanos?
Solución:
Incógnitas:
- \(x\) es la edad de María
- \(y\) es la edad de Miguel
Ecuaciones:
La edad de María dentro de 3 años es \(x+3\), que es la misma que la edad de Miguel:

La edad de Miguel dentro de 10 años es \(y+10\), que es el doble de la edad de María:
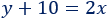
Sistema de ecuaciones:
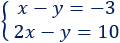
La solución del sistema es
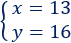
La edad de María es 13 y la de Miguel es 16.
Problema 3
Un rectángulo tiene perímetro 8 metros y su altura es el triple que su base. ¿Cuál es la altura del rectángulo?
Solución:
Incógnitas:
- \(x\) es la base
- \(y\) es la altura
Ecuaciones:
La altura es el triple que la base:
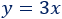
El perímetro es la suma de sus cuatro lados:
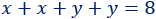
Es decir,

Sistema de ecuaciones:
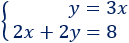
La solución del sistema es
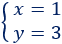
Por tanto, la altura mide 3 metros.
Problema 4
Hallar un número de dos cifras sabiendo que la suma de sus cifras es 12 y que la segunda es el doble de la primera.
Solución:
Incógnitas:
- \(x\) es la primera cifra
- \(y\) es la segunda cifra
Ecuaciones:
La suma de las cifras es 12:
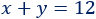
La segunda cifra es el doble de la primera:
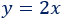
Sistema de ecuaciones:
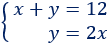
La solución del sistema es
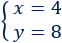
Por tanto, es el número 48.
Problema 5
Un equipo de básquet anotó un total de 55 canastas, obteniendo 125 puntos. ¿Cuántos tiros de campo (2 puntos) y triples (3 puntos) realizaron?
Solución:
Incógnitas:
- \(x\) es el número de tiros de campo
- \(y\) es el número de tiros triples
Ecuaciones:
La suma total de tiros es 55:
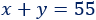
El tiro de campo suma 2 puntos y el triple suma 3, siendo 125 el total de puntos:
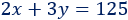
Sistema de ecuaciones:
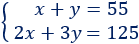
La solución del sistema es
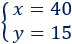
El equipo realizó 40 tiros de campo y 15 triples.
Problema 6
Carla gastó 154€ en camisetas y pantalones. Si el precio de cada camiseta era de 2€ y el de cada pantalón era de 8€ y compró 3 camisetas por cada pantalón, ¿qué cantidad de camisetas y pantalones compró?
Solución:
Incógnitas:
- \(x\) es el número de camisetas
- \(y\) es el número de pantalones
Ecuaciones:
El coste total es de 154:
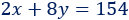
El número de camisetas es el triple que el de pantalones:
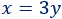
Sistema de ecuaciones:
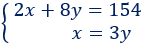
La solución del sistema es
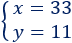
Carla compró 33 camisetas y 11 pantalones.
Problema 7
Juana mide 23cm más que Guadalupe y la altura promedio de ambas amigas es 151.5cm. ¿Cuánto mide Guadalupe?
Solución:
Incógnitas:
- \(x\) es la altura de Juana
- \(y\) es la altura de Guadalupe
Ecuaciones:
La altura promedio es 151.5:
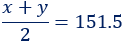
Juana mide 23cm más que Guadalupe:
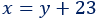
Sistema de ecuaciones:
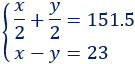
La solución del sistema es
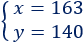
Juana mide 163cm.
Problema 8
Cortamos una cuerda de 60cm en 5 trozos. Hay 3 trozos cortos que miden lo mismo y los otros 2 trozos miden 5cm más que los cortos. ¿Cuánto miden los trozos?
Solución:
Incógnitas:
- \(x\) es la longitud de los trozos pequeños
- \(y\) es la longitud de los trozos grandes
Ecuaciones:
La longitud que suman todos los trozos es 60:
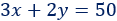
Los trozos grandes miden \(5\)cm más que los pequeños:
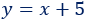
Sistema de ecuaciones:
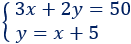
La solución del sistema es
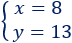
Los trozos cortos miden 8cm y los largos miden 13cm.
Problema 9
Hace 5 años, la edad de Maribel era la cuarta parte de la edad de su madre. Dentro de 5 años, su edad será la mitad que la de su madre. ¿Qué edad tiene Maribel?
Solución:
Incógnitas:
- \(x\) es la edad actual de Maribel
- \(y\) es la edad actual de la madre
Ecuaciones:
Hace 5 años, las edades de Maribel y de su madre eran \(x-5\) e \(y-5\). La edad de la hija era la cuarta parte:
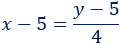
Dentro de 5 años, serán \(x+5\) e \(y+5\). La edad de la hija será la mitad:
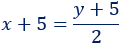
Sistema de ecuaciones:
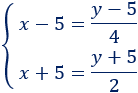
La solución del sistema es
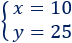
Maribel tiene 10 años.
Problema 10
En la nevera tenemos botellas de agua de 2L y de 3L. Si las 8 botellas que tenemos suponen un total de 19L, ¿cuántas botellas tenemos de cada tamaño?
Solución:
Incógnitas:
- \(x\) es el número de botellas de 2L
- \(y\) es el número de botellas de 3L
Ecuaciones:
Tenemos 9 botellas:
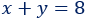
En total de agua es 19L:
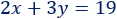
Sistema de ecuaciones:
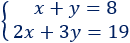
La solución del sistema es
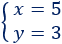
Tenemos 5 botellas de 2L y 3 botellas de 3L.