Problemas de porcentaje de diferencia o de error
Explicamos el concepto de porcentaje de diferencia o de error (con y sin signo) y resolvemos problemas de aplicación. Para calcular los porcentajes, aplicamos una regla de tres (más información en calcular porcentajes).
Básicamente, el porcentaje de diferencia nos indica en qué porcentaje varía una cantidad respecto de otra.
Ejemplo 1: Si en nuestra hucha había 100€ y ahora hay 50€, el porcentaje de diferencia es el 50% porque la cantidad que ha disminuido es la mitad del dinero inicial:

Fórmula
Para calcular el porcentaje de diferencia, usamos la siguiente fórmula:
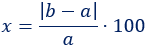
donde \(a\) es la cantidad inicial y \(b\) es la final.
El porcentaje de diferencia es el porcentaje que ha aumentado o disminuido la cantidad inicial.
La fórmula anterior es la regla de tres que utilizamos para calcular qué porcentaje es \(|b-a|\) con respecto de \(a\):
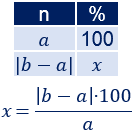
Ejemplo 2: Si en nuestra hucha había 50€ y ahora hay 100€, el porcentaje de diferencia es el 100% porque la cantidad ha aumentado el 100% del dinero inicial:
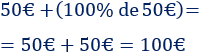
Importante
El porcentaje de diferencia del cambio de \(a\) a \(b\) no es igual al porcentaje de diferencia del cambio de \(b\) a \(a\), excepto si \(a=b\). Esto podemos observarlo en los ejemplos anteriores.
A partir del Problema 4, explicamos cómo calcular el porcentaje de diferencia con signo, lo que permite determinar si la cantidad inicial crece o decrece.
Porcentaje de error
Cuando una cantidad es una aproximación de otra, el porcentaje de diferencia suele llamarse porcentaje de error.
Problema 1
Calcular el porcentaje de diferencia entre 60 (inicial) y 48 (final).
Solución:
Calculamos el valor absoluto de la resta final menos inicial:
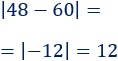
Dividimos entre la cantidad inicial y multiplicamos por 100:
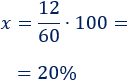
El porcentaje de diferencia es el 20%. Es decir, la cantidad inicial ha disminuido un 20%.
Problema 2
Calcular el porcentaje de diferencia entre 140 (inicial) y 196 (final).
Solución:
Calculamos el valor absoluto de la diferencia de ambas cantidades, dividimos por la inicial y multiplicamos por 100:
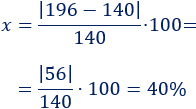
El porcentaje de diferencia es el 40%. Es decir, la cantidad inicial ha aumentado un 40%.
Problema 3
Calcular el porcentaje de diferencia entre
-
80 (inicial) y 96 (final)
-
80 (inicial) y 64 (final)
Solución:
-
80 y 96
Aplicamos la fórmula:
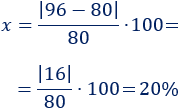
-
80 y 64
Aplicamos la fórmula:
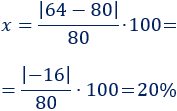
En el primer apartado, el porcentaje de diferencia es un aumento. En el segundo, es una disminución. En ambos casos, el porcentaje de diferencia es el mismo.
Si eliminamos el valor absoluto, la fórmula es
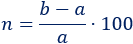
De este modo, el resultado es positivo cuando \(a\) sufre un aumento y es negativo cuando sufre una disminución.
Problema 4
Calcular el porcentaje de diferencia (con signo) entre
-
80 (inicial) y 96 (final)
-
80 (inicial) y 64 (final)
Solución:
-
80 y 96
Aplicamos la fórmula:
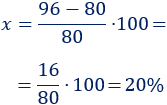
-
80 y 64
Aplicamos la fórmula:
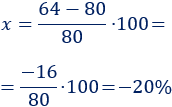
En el primer apartado, el porcentaje de diferencia es positivo porque representa un aumento del 20%. En el segundo, es negativo porque representa una disminución del 20%.
Problema 5
¿Cuál es el porcentaje de diferencia (con signo) de los beneficios de una empresa si han antes eran 120 millones anuales y ahora son 108 millones?
Solución:
Aplicamos la fórmula:
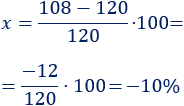
Como el porcentaje de diferencia es -10%, los beneficios han caído un 10%.
Problema 6
Si los beneficios de una empresa de este año son el 75% de los beneficios del año pasado, ¿cuál es el porcentaje de diferencia (con signo)?
Solución:
Si los beneficios son el 75%, ha habido un descenso del 25%. Por tanto, el porcentaje de diferencia es el -25%.
Problema 7
Los beneficios de este año de una empresa son 69 millones anuales y el porcentaje de diferencia (con signo) de los beneficios con respecto al año pasado es del 15%, ¿qué beneficios tuvo la empresa el año pasado?
Solución:
Como el porcentaje es positivo, los beneficios han subido un 15% respecto del año anterior. Por tanto, los 69 millones de este año son el 115% del año pasado.
Calculamos los beneficios del año pasado aplicando una regla de tres:

Los beneficios del año pasado fueron 60 millones. Las ganancias de este año han aumentado en 9 millones.
Problema 8
Si un porcentaje de diferencia (con signo) del 25% supone que una cantidad ha aumentado en 30 unidades, ¿cuál era la cantidad inicial? ¿Y la final?
Solución:
El porcentaje de diferencia del 25% nos indica el 25% de la cantidad inicial. Calculamos el 100%:
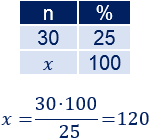
La cantidad inicial era 120. Por tanto, la final es 150.
Problema 9
Si un porcentaje de diferencia (con signo) del -25% supone que una cantidad ha disminuido en 30 unidades, ¿cuál era la cantidad inicial? ¿Y la final?
Solución:
Un porcentaje de diferencia del -25% nos proporciona el 25% de la cantidad inicial. Calculamos el 100%:
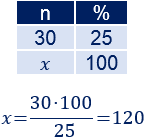
La cantidad inicial era 120. Por tanto, la final es 90.
Problema 10
En una tienda, rebajan el precio de un artículo al 70%. ¿Cuál es el porcentaje de diferencia (con signo) del precio de dicho artículo?
Solución:
El precio inicial es el 100%.
El precio final es el 70%.
Por tanto, se aplica un descuento del 30%.
El porcentaje de diferencia (con signo) es del -30%.