Métodos para resolver sistemas de ecuaciones
Explicamos los 4 métodos básicos para resolver un sistema de ecuaciones lineales:
- Método de sustitución
- Método de igualación
- Método de reducción
- Método gráfico
Resolvemos como ejemplo un sistema de 2 ecuaciones lineales con 2 incógnitas utilizando cada uno de los métodos.
Importante: para resolver un sistema con \(n\) incógnitas se necesitan, al menos, \(n\) ecuaciones.
Nota: existen otros métodos de resolución de sistemas, por ejemplo, entre los más sencillos tenemos (álgebra matricial):
Recursos complementarios:
1. Método de sustitución
Este método consiste en aislar una incógnita en una de las ecuaciones para sustituirla en la otra ecuación. De este modo, se obtiene una ecuación con una sola incógnita. Una vez resuelta esta ecuación, se sustituye en alguna de las ecuaciones para hallar la otra incógnita.
Ejemplo:
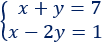
Despejamos la \(x\) en la primera ecuación:
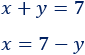
Ahora, sustituimos la expresión algebraica en la segunda, es decir, escribimos \(7-y\) donde aparece \(x\):
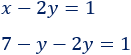
Resolvemos la ecuación:
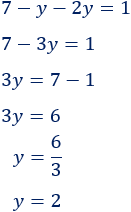
Como ya conocemos \(y\), podemos calcular \(x\) a partir de la ecuación que obtuvimos al despejar \(x\):
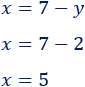
Por tanto, la solución del sistema es \(x=5\) e \(y=2\):
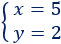
2. Método de igualación
Este método consiste en despejar la misma incógnita en las dos ecuaciones para igualar las expresiones algebraicas obtenidas. Se obtiene, así, una ecuación con una incógnita.
Ejemplo:
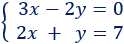
Despejamos la \(x\) en la primera ecuación:
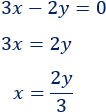
Despejamos la \(x\) en la segunda ecuación:
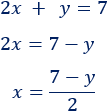
Igualamos las dos expresiones:
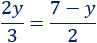
Resolvemos la ecuación obtenida:
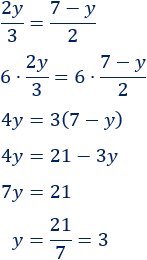
Como conocemos \(y\), podemos calcular \(x\) (sustituyendo):
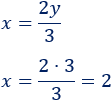
Por tanto, la solución del sistema es
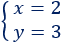
3. Método de reducción
Este método consiste en sumar (o restar) las ecuaciones entre sí para eliminar una de las incógnitas. A veces, es necesario multiplicar por algún número las ecuaciones para que, al sumarlas, desaparezca una de las incógnitas.
Ejemplo:
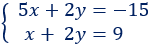
Como las dos ecuaciones tienen el monomio \(2y\), si las restamos, éste desaparece:
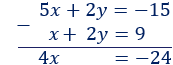
Nota: si hubiésemos querido eliminar la incógnita \(x\), tendríamos que haber multiplicado la segunda ecuación por 5 antes de restar las ecuaciones.
Resolvemos la ecuación:
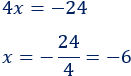
Calculamos la otra incógnita sustituyendo en alguna de las ecuaciones (la segunda, por ejemplo):
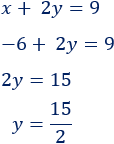
Por tanto, la solución del sistema es
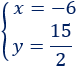
4. Método gráfico
Este método consiste en representar las dos ecuaciones y calcular el punto de corte de las mismas. Este punto es la solución del sistema porque sus coordenadas cumplen ambas ecuaciones.
Ejemplo:
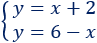
Representación de las gráficas de las dos ecuaciones:
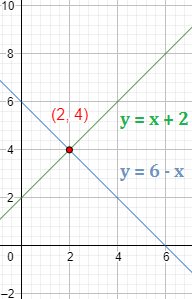
El punto de corte entre las rectas (intersección) es (2,4).
Como la primera coordenada es la \(x\) y la segunda es la \(y\), la solución del sistema es
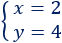
¡Si no hay punto de corte, el sistema no tiene solución!