Problemas resueltos de porcentajes de aumentos o incrementos
Resolvemos problemas de porcentajes de aumentos o incrementos. Usaremos, en algunos problemas, porcentajes mayores que 100%.
Para calcular los porcentajes, utilizamos una regla de tres. Más información en Calcular porcentajes (teoría y ejemplos).
Problema 1
El año pasado se vendieron 1200 videojuegos y 980 libros. Si este año subió un 15% la venta de videojuegos y subió un 5% la de libros, ¿cuántos videojuegos y libros se vendieron?
Solución:
Como la venta de videojuegos aumentó un 15%, la venta fue del 115%:

Este año se vendieron 1380 videojuegos.
También, podríamos haber calculado el 5% y sumarlo.
Como la venta de libros subió un 5%, la venta fue del 105%:
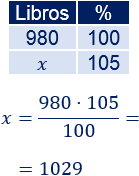
Este año se vendieron 1029 libros.
Problema 2
Daniel tenía 260€ en su hucha y en dos meses consiguió ahorrar otro 55% del dinero que ya tenía. ¿Cuánto dinero ahorró en los dos meses?
Solución:
En este problema no queremos saber el total al añadir el 55%, sino calcular el 55% del dinero inicial:

Daniel ahorró 143€ en esos dos meses.
Problema 3
La nota media de María pasó de ser un 5 a ser un 6. ¿Qué porcentaje aumentó su nota?
Solución:
La diferencia entre las notas es de 1 punto:

La nota de María subió un 20%.
Problema 4
La temperatura media anual en una determinada localidad es de 20°C. Si la media aumenta un 2%, ¿cuántos grados aumentaría la temperatura media?
Solución:
Los 20 grados es el 100%. Calculamos el 2%:

Un incremento del 2% en la temperatura sería un aumento de 0.4°C.
Problema 5
El número de libros de Joana este año es un 35% superior al del año anterior. Si ahora tiene 810 libros, ¿cuántos libros tenía Joana el año pasado?
Solución:
Como hubo un incremento del 35%, ahora tiene el 135% comparando con el año anterior:

El año pasado Joana tenía 600 libros.
Problema 6
El aumento del sueldo de Carlos del 15% supone que ahora cobra 204€ más. ¿Cuál era su sueldo antes del aumento?
Solución:
Sabemos que el 15% del sueldo anterior son 204€:

El sueldo de Carlos antes del aumento era de 1360€.
Problema 7
Mariela efectuaba 50 saltos en 1 minuto y ahora efectúa 60 en el mismo tiempo. ¿Cuál es el porcentaje del incremento?
Solución:
Mariela ahora efectúa 10 saltos más que antes:

Mariela ha incrementado un 20% el número de saltos.
Problema 8
Tras 2 meses de entrenamiento, Felipe consiguió subir el número de abdominales por minuto de 35 a 63. ¿Qué porcentaje de abdominales hace ahora con respecto a 2 meses atrás? ¿Cuál es el porcentaje del incremento?
Solución:
Como hace más abdominales por minutos, el porcentaje es mayor que 100%:
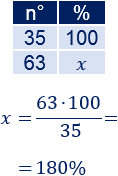
El número de abdominales por minuto que hace ahora Felipe es el 180% del que hacía antes. Esto supone un incremento del 80%.
Problema 9
En 2010, el precio de la vivienda subió un 10%. En 2011, subió un 5%. ¿Cuál era el precio de una vivienda en 2011 si en 2009 era de 80000€? ¿Subió el precio un 15% en estos dos años? ¿Por qué?
Solución:
En 2010 subió un 10%:

En 2010 el precio era de 88000€.
En 2011 subió un 5%:

El precio en 2011 era de 92400€.
Calculamos el precio de la vivienda si hubiese subido un 15% el precio inicial:

El precio habría sido de 92000.
Un incremento del 5% en el precio después de un incremento del 10% no es un incremento del 15% en el precio inicial. Esto se debe a que el incremento del 5% se aplica sobre el precio ya incrementado en un 10%.
Problema 10
La siguiente tabla recoge el número de habitantes en las localidades A y B en los años 2005, 2010 y 2015:
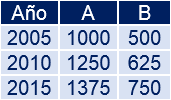
Contestar:
-
Comparando 2005 con 2010, ¿en qué localidad hubo un aumento mayor?
-
Comparando 2010 con 2015, ¿en qué localidad hubo un aumento mayor?
-
Comparando 2005 con 2015, ¿en qué localidad hubo un aumento mayor?
Solución:
Para no escribir tantas tablas, usaremos tablas dobles, pero no significa que vayamos a aplicar reglas de tres compuestas. Las operaciones son las mismas.
Calculamos el incremento entre 2005 y 2010:

Entre 2005 y 2010, el incremento es del 25% en ambas localidades.
Calculamos el incremento entre 2010 y 2015:

Entre 2010 y 2015, el incremento es del 10% en la localidad A y del 20% en la B. Hubo un mayor incremento en la localidad B.
Calculamos el incremento entre 2005 y 2015:
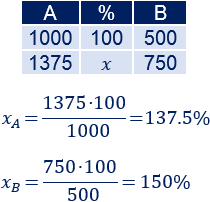
Entre 2005 y 2015, el incremento es del 37.5% en la localidad A y del 50% en la B. El incremento en la localidad B es mayor.